はじめに
こんにちは!ひらちんです!Rを使った統計について自分の勉強も兼ねて記事にしています。
今回は、確率分布の中の一番大事な正規分布です。
正規分布
統計の勉強を始めたら最初に出てくる一番大事な確率分布
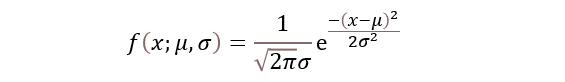
μ:平均 σ:標準偏差 e:ネイピア数
こんなやつ。
気が狂ったような数式で難しいっすね。
正規分布からランダムに数字を生成する
正規分布に従った数字をランダムに生成したい場合 rnorm関数 を使います。
平均μと標準偏差σを指定出来ます。
rnorm(n, mean, sd)
# 平均μ 15 標準偏差σ 20 の正規分布 N(15, 20^2)に従う数字を10個生成
rnorm(n=10 , mean=15, sd=20)みたいな感じ。

ランダムなんで、もう一回やると違う数字が抽出されるね。
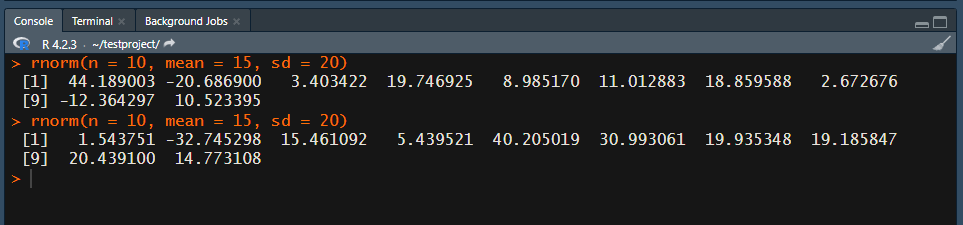
ちなみに、引数のmean(平均)とsd(標準偏差)を指定しないと、標準正規分布 N(0, 1)に従う数字を抽出します。(nは指定しないと怒られるので、nだけは指定してあげてください。)
# 引数のn(抽出数)だけ指定して実行する
rnorm(n=10)
まぁ、ぱっと見でこれが標準正規分布に従っている数字だなんて分かんないから、おおーっ!ともならないね(笑)
ふふーん。。。ぐらい
正規分布の確率密度を計算する
正規分布における、その値の確率密度(出現確率)を計算するには、 dnorm関数 を使います。
つまり、さっき出てきたこいつを計算するんですね。
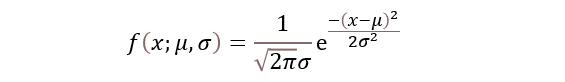
例えば、標準正規分布のxが0のときの出現確率は
dnorm(0, mean=0, sd=1)
で「0.3989423」となります。

一応、みんな大好きExcel君でも確認しときます?
Excelでは、 PHI関数 で標準正規分布の確率密度を計算することが出来ます。
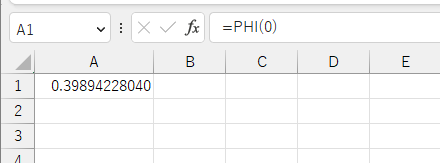
おんなじくらいですね。
ということで、さっき rnorm関数 でランダムに作ったたくさんの数字を、 dnorm関数 の引数に入れてやればそれぞれ計算してくれると言うわけですね。
ちなみに、 dnorm関数 も引数のmean(平均)とsd(標準偏差)を指定しないと、標準正規分布 で計算してくれます。
では、 rnorm関数 で標準正規分布に従う数値をいっぱい作って、それの確率密度を dnorm関数 で計算して、せっかくなのでグラフにしてみます!
# rnorm関数で、標準正規分布に従った数字をたくさん作る(ここでは10000個)
rnorm10000 <- rnorm(n=10000)
# 生成した数字達を dnorm関数に入れる
dnorm10000 <- dnorm(rnorm10000)
# グラフ作成用に ggplot2 をロードする
require(ggplot2)
# グラフを描画
ggplot(data.frame(x = rnorm10000, y = dnorm10000)) +
aes(x = x, y = y) +
geom_point() + labs(x = "正規分布", y = "確率密度")こんな感じですね。
ggplot2 は、グラフとか作るときに便利なやつです。
出来たグラフはこれです。
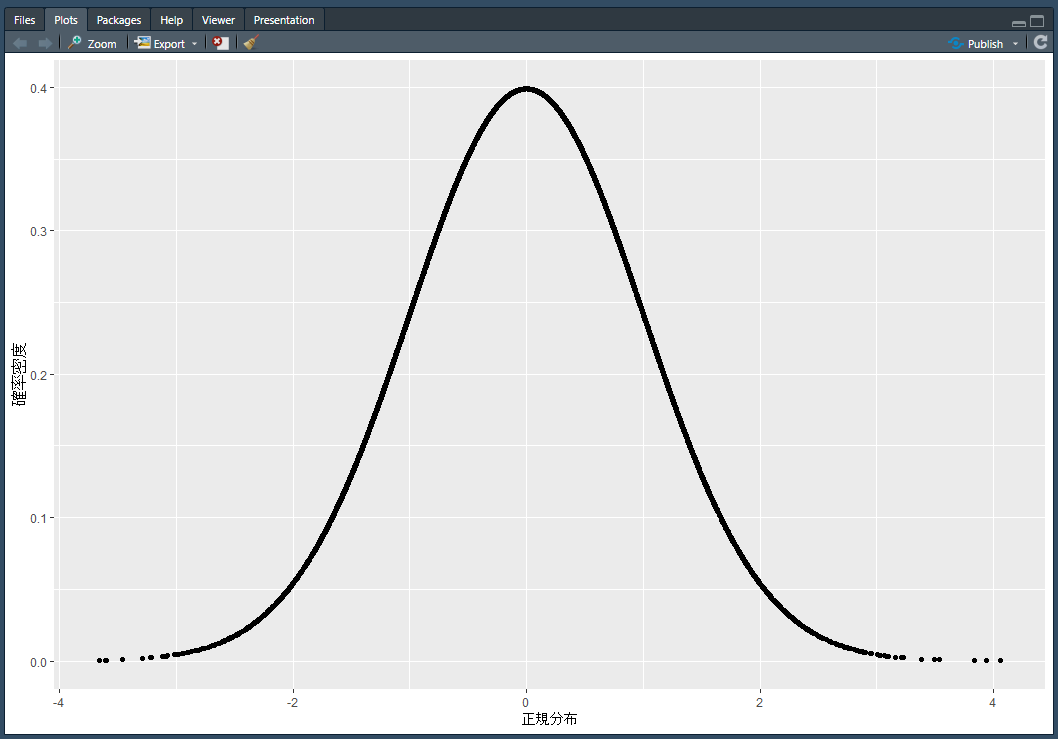
両端はぷつぷつしてますが、釣鐘型のきれいなグラフが描けました!
正規分布の累積確率を計算する
dnorm関数 はxに対する確率密度を計算してくれましたが、そのxまでの累積確率を計算する pnorm関数 も用意されています。
累積確率の定義は、次です。
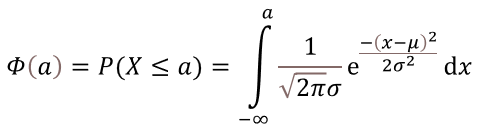
正規分布の数式を積分してるだけですね。
つまり、これを計算してくれます。
では、標準正規分布のxが0のところまでの累積確率を計算してみましょう!
pnorm(0, mean=0, sd=1)
で「0.5」となります。

さっき描いたグラフのxが0以下の部分なんで、0.5ですね。
0は真ん中です。
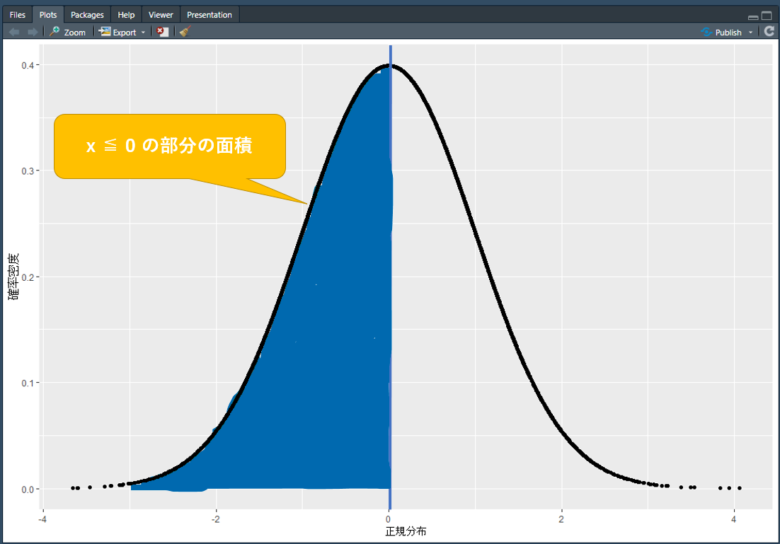
では、せっかくなので累積確率もグラフにしてみましょう!
dnorm関数 でやったときと基本的には同じです。
dnorm関数 のところを pnorm関数 に変えています。
# rnorm関数で、標準正規分布に従った数字をたくさん作る(ここでは10000個)
rnorm10000 <- rnorm(n=10000)
# 生成した数字達を pnorm関数に入れる
pnorm10000 <- pnorm(rnorm10000)
# グラフ作成用に ggplot2 をロードする
require(ggplot2)
# グラフを描画
ggplot(data.frame(x = rnorm10000, y = pnorm10000)) +
aes(x = x, y = y) +
geom_point() + labs(x = "正規分布", y = "累積確率密度")出来たグラフはこれです。
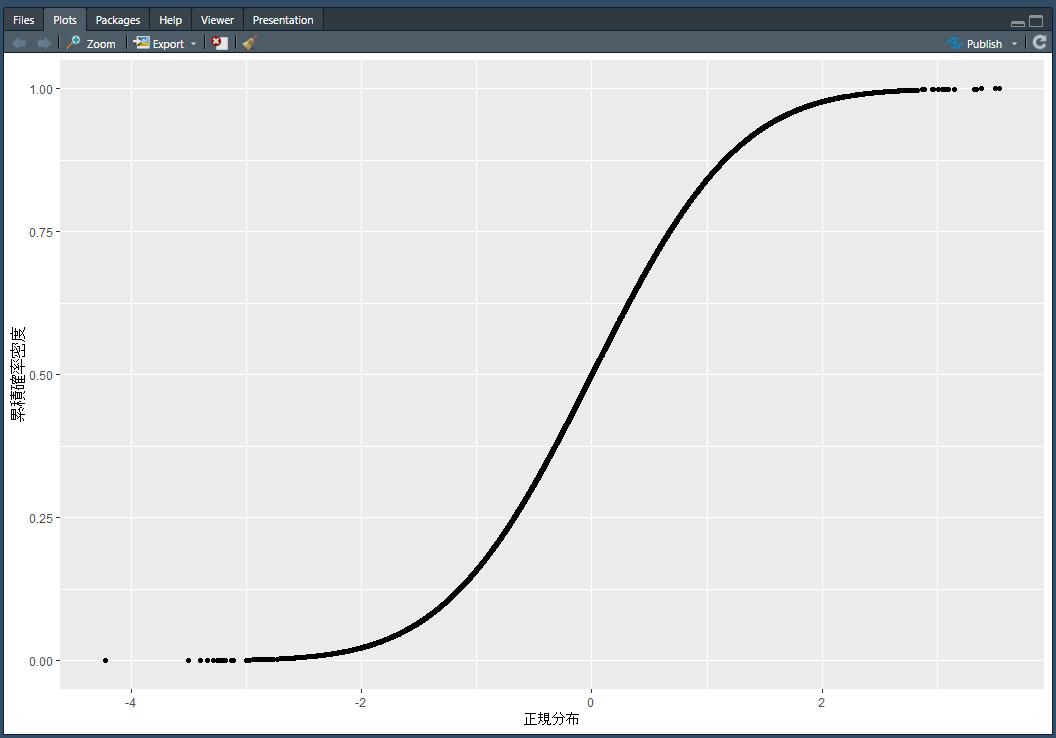
累積確率なので、どんどん増えていって、最後は1に近づきますね。
まとめ
今回は、Rでの正規分布について勉強しました。
累積密度のところでは、グラフに手塗りをしましたが、Rはグラフ表現をするための方法もたくさんあるので、グラフ内を塗りつぶしたりも出来ます。
また、機会があれば紹介します!
コメント