はじめに
こんにちは!ひらちんです!Rを使った統計について自分の勉強も兼ねて記事にしています。
今回は、コインの表と裏でお馴染みの二項分布です!
ベルヌーイ試行
二項分布の前に、ベルヌーイ試行についてです。
ベルヌーイ試行と言うのは「成功or失敗」「表or裏」「勝ちor負け」みたいに2種類のみの結果しか得られないような試行のことを言います。
1回コインを投げたとき、“表”が出るか“裏”が出るか、みたいなのが代表的なやつですね。
通常コインだと、表も裏も50%ずつの確率で出る感じですが、確率は50%ずつで無くてもOKです。
何回やっても1回1回が同じ確率だったら良いわけです。
成功確率[表の確率]をpとすると、失敗確率[裏の確率]は(1-p)となりますね。
二項分布
で、二項分布というのは、 そのベルヌーイ試行をn回行ったときに、ある事象が何回起こるかの確率分布を言います。
例えば、コイン10回投げたときに、
表が0回出る確率、表が1回出る確率、表が2回出る確率、表が3回出る確率、、、、表が10回出る確率、みたいな確率の分布です。
コイン10回投げた場合の表が出る回数のそれぞれの確率を計算すると、、、
成功回数は0回から10回まで、表が出る確率Pは0.5なので全部計算すると以下のような形になりますね。
| 成功回数 x | 確率 f(x) | 計算式 |
|---|---|---|
| 0 | 0.001 | 1 ✕ 0.5^0 ✕ (1-0.5)^10 |
| 1 | 0.010 | 10 ✕ 0.5^1 ✕ (1-0.5)^9 |
| 2 | 0.044 | 45 ✕ 0.5^2 ✕ (1-0.5)^8 |
| 3 | 0.117 | 120 ✕ 0.5^3 ✕ (1-0.5)^7 |
| 4 | 0.205 | 210 ✕ 0.5^4 ✕ (1-0.5)^6 |
| 5 | 0.246 | 252 ✕ 0.5^5 ✕ (1-0.5)^5 |
| 6 | 0.205 | 210 ✕ 0.5^6 ✕ (1-0.5)^4 |
| 7 | 0.117 | 120 ✕ 0.5^7 ✕ (1-0.5)^3 |
| 8 | 0.044 | 45 ✕ 0.5^8 ✕ (1-0.5)^2 |
| 9 | 0.010 | 10 ✕ 0.5^9 ✕ (1-0.5)^1 |
| 10 | 0.001 | 1 ✕ 0.5^10 ✕ (1-0.5)^0 |
これのことです。
数学的に、確率質量関数を書くと、、、こんなやつ。
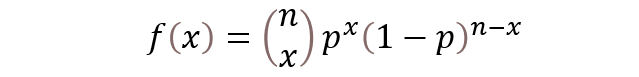
こんな風に書いてる場合もありますね。
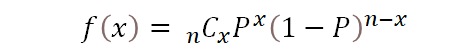
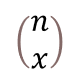
こいつは、大学で数学やってないと馴染みないと思いますが、以下のようなことです。
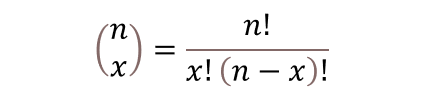
2つ目に書いた式の
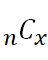
と同じことですね。つまり組み合わせの数ってことです。
数学詳しい人に言わせると厳密には違うようですが、、、まぁここでは同じってことで良いでしょう(^o^)
二項分布から乱数を生成する
さぁ、ここからがややこしいですよ。
ある二項分布から乱数を生成するって言うことは、単に乱数を生成するということでは無くて、
になります。
何を言ってるかというと、、、
でしたね。
「表1」で言うところの、成功回数 x のところがある二項分布に従った形でランダムに出ないといけないという分けです。
R では rbinom関数 を使って生成します。
rbinom(n=1, size=10, prob=0.5)
のような感じです。
って言う意味になります。
つまり、nに指定した回数の試行結果が返ってくることになります。
計算してくれるっていうのではなくて、代わりに試行してくれるっていう理解で良いと思います。
なので、このコードは実行する度に答えが違います。
やってみましょう!
先程のこのコードです。
rbinom(n=1, size=10, prob=0.5)

1回実行したら、結果は「7」でした。
もう一回やってみます。

2回目は、結果は「6」でした。
念のためもう1回w
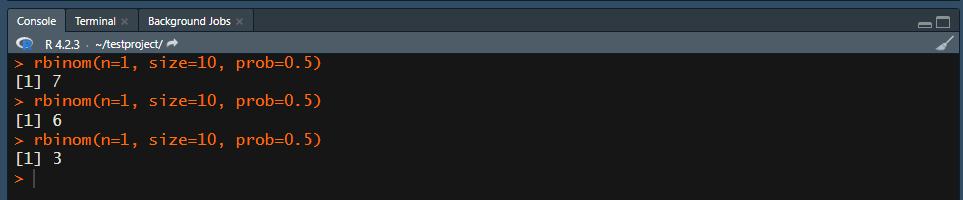
3回目は「3」でした。
このように、代わりに実験して見てくれるってことですね。
ちなみに、1回1回実行しなくても、「n=20」とかにすれば20回一気にやってくれます。
じゃんっ!
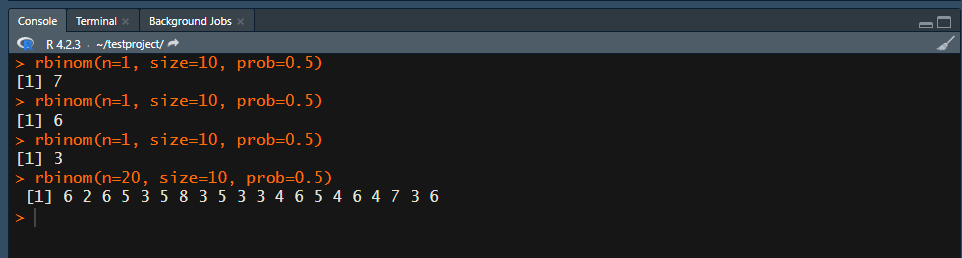
これで終わっても何なんで、とりあえずグラフにしてみましょう!
コード的には
rbinom(n=10000, size=10, prob=0.2)
です。
で、こいつを data.frame にして、グラフ化するってイメージです。
# rbinomで生成した結果をデータフレームに打ち込む
df <- data.frame(d <- rbinom(n=10000, size=10, prob=0.2))
# グラフの作成
require(ggplot2)
ggplot(df, aes(x = d)) + geom_histogram(binwidth = 1)何回か実行している動画をご覧下さい。
こんな感じのグラフが生成されました。
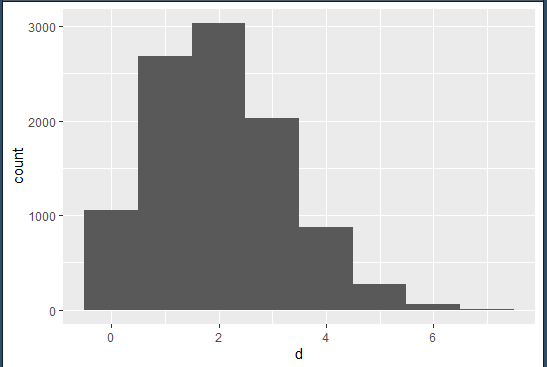
予想通り「2」に一番ボリュームのあるグラフが出来上がりますね(^o^)
二項分布は、試行回数(n)を大きくしていくと正規分布に近似していきます。
成功回数xの確率を計算する
コイン10回投げて、表が4回出る時の確率って?みたいな計算の方が実際には多いかもしれません。
そんなときは dbinom関数 を使います。
要するに、冒頭に記した↓の計算をしてくれるってわけです。
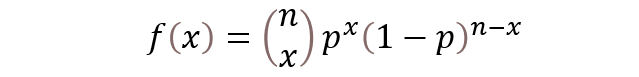
dbinom(x=4, size=10, prob=0.5)
rbinom関数 に似てますが、nのところがxになってますね。
ここに、確率計算したい成功回数を指定します。
ここでは、4回に設定しています。
では実行してみましょう!
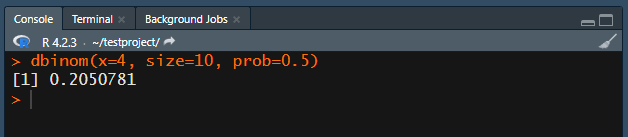
はい。
「表1」と違うじゃん!って思うかもしれませんが、「表1」は丸め込みしてるので一緒です!w
他も一応やってみます。
dbinom(x=0:10, size=10, prob=0.5)
何回もやるの面倒なので、「x=1:10」で一気にやります。
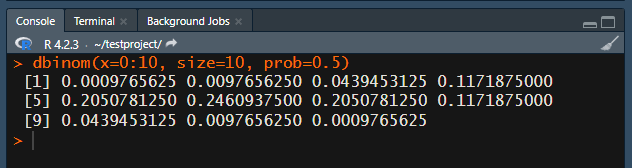
「表1」と同じじゃ無いけど同じです!w
累積確率を計算する
最後に、成功回数が4回以下の確率を計算する場合もやっときます。
4回以下の確率ということは、0回か1回か2回か3回か4回成功する(表が出る)ということなので、確率は0回~4回までの成功確率を全部足したら良いですね。
いわゆる累積確率ってやつです。
表にするとこんな感じです。
| 成功回数 x | 確率 f(x) | 累積確率 F(x) |
|---|---|---|
| 0 | 0.001 | 0.001 |
| 1 | 0.010 | 0.011 |
| 2 | 0.044 | 0.055 |
| 3 | 0.117 | 0.172 |
| 4 | 0.205 | 0.377 |
| 5 | 0.246 | 0.623 |
| 6 | 0.205 | 0.828 |
| 7 | 0.117 | 0.945 |
| 8 | 0.044 | 0.989 |
| 9 | 0.010 | 0.999 |
| 10 | 0.010 | 1 |
累積確率を計算する時の関数は以下です。
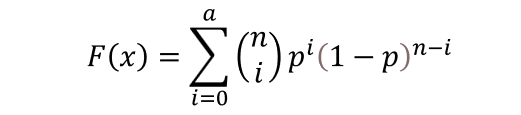
つまりこれを計算するための関数です。
Rで二項分布からの累積確率を計算するのは pbinom関数 になります。
pbinom(q=4, size=10, prob=0.5)
使い方は、引数のqに、どこまでの累積かを入れればいいだけです。
今回は、4回以下としたいので「4」を指定しています。
では実行してみましょう!

はい。
「0.3769531」と出ました。
表2で計算したものは、「0.377」でしたので丸めの誤差はありますが一緒ですね!
0~10まで全部確認してみましょう!
pbinom(q=0:10, size=10, prob=0.5)
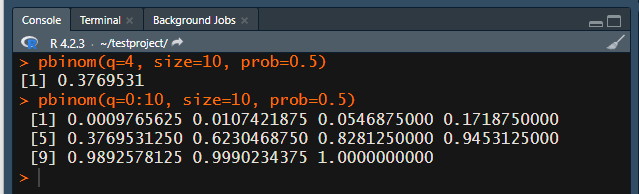
一緒ですね(^o^)
まとめ
今回は、Rでの二項分布について勉強しました。
まだまだ、先は長いが頑張るぞ!
コメント