はじめに
こんにちは!ひらちんです!Rを使った統計について自分の勉強も兼ねて記事にしています。
今回は、分位点(分位数)についてです!
分位点(分位数)
分位点(分位数)とは、
ってやつです!
つまり中央値は50%分位点となりますね(^o^)
次のサンプルを使って説明したいと思います。
| 名前 | 身長 |
|---|---|
| Aさん | 171cm |
| Bさん | 177cm |
| Cさん | 169cm |
| Dさん | 165cm |
| Eさん | 172cm |
| Fさん | 174cm |
| Gさん | 188cm |
| Hさん | 190cm |
| Iさん | 175cm |
| Jさん | 169cm |
| Kさん | 183cm |
このデータを小さいもん順に並べると
| 1 | 2 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| D | C | J | A | E | F | I | B | K | G | H |
| 165 | 169 | 169 | 171 | 172 | 174 | 175 | 177 | 183 | 188 | 190 |
こんな順番になりますね。
50%の場所にあるのは6番目のFさんです。
| 1 | 2 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| D | C | J | A | E | F | I | B | K | G | H |
| 165 | 169 | 169 | 171 | 172 | 174 | 175 | 177 | 183 | 188 | 190 |
つまり、174になりますね
こんな感じです。
Rで分位点を算出するには、 quantile関数を使います。
quantile(x = x, probs = 0.5)
xは先程の表をベクトルで作成しています。
probsに、分位点を出したい値を%で指定します。
ここでは、中央なので50%を指定しています。
では実行してみましょう。
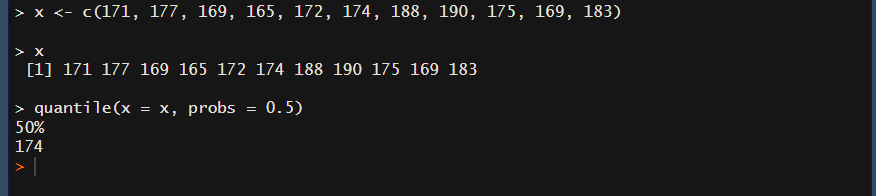
真ん中の数値174が返されましたね(^o^)
分かりやすく図にするとこんな感じ。

データの真ん中なので問題ないですね。
では、データ数が偶数のときはどうでしょうか。
奇数の場合は、ちょど良く真ん中がありません。。。
一旦、どうなるか確認してみましょう。
先程のデータに155を追加したデータを変数yに入れておきます。
y <- c(171, 177, 169, 165, 172, 174, 188, 190, 175, 169, 183, 155)
順番は次のようになりますね。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 13 |
| L | D | C | J | A | E | F | I | B | K | G | H |
| 155 | 165 | 169 | 169 | 171 | 172 | 174 | 175 | 177 | 183 | 188 | 190 |
それでは実行してみます。
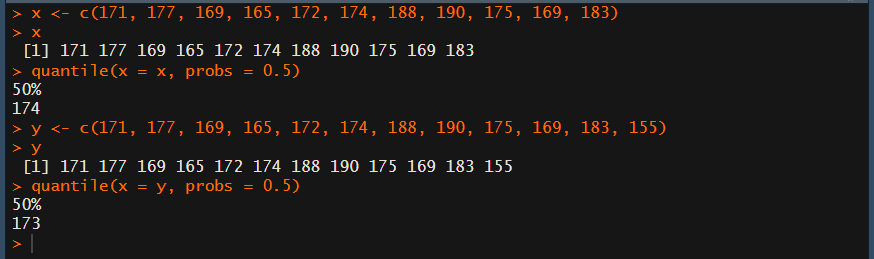
yは後半のところです。
結果は、173となりました。
この場合は以下のように考えます。
データの真ん中は無いので、真ん中の2つの数字を使います。

この例では、172と174が該当します。
この2つの数字の平均したものが答えになります。
(172+174)÷2=173
中央値と同じなので大丈夫ですね(^o^)
四分位点(四分位数)
分位点で一番有名なのは、四分位点ですね。
データを4つに分けた時のそれぞれの区切り目の数です。
箱ひげ図作るときなんかにも利用します。
最小値 ・・・0%
第1四分位点・・・25%
第2四分位点・・・50%
第3四分位点・・・75%
最大値 ・・・100%
ような感じでデータを4つに分けた時の各分位点です。
quantile関数は引数probsを指定しないと上記の分位点を表示します。
先程のデータx(11個のデータ)で実行してみます。
quantile(x = x)

出ましたね。
先ほどと同じ図で表すと次のようになります。

最小値・第2四分位点・最大値は大丈夫ですね。
では、第1四分位点と第3四分位点についてはどのように計算されているでしょうか。
実は、四分位数には複数定義がありますので、どの定義の四分位数を使っているのかで数値が変わってきます。
ここでは quantile関数のデフォルト状態でどのように計算されているかを説明します。
※その他の定義:文部科学省推奨とか箱ひげ図考案者Tukeyさんの定義とかあります。
まずは算出方法から
データを x1, x2, x3, … , xk とした時
①「k(データ数) – 1 」に 0.25(第1四分位点), 0.5(第2四分位点), 0.75(第3四分位点)を掛ける。
②①の値が
【整数】その番号のデータがそれぞれ第1四分位数,中央値,第3四分位数になる。
【整数+0.25】その数より1つ大きい数kと k+1番目の値で調整する。
0.75 ✕ xk + 0.25 ✕ xk+1
【整数+0.5】その数より1つ大きい数kと k+1番目の値で調整する
0.5 ✕ xk + 0.5 ✕ xk+1
【整数+0.75】その数より1つ大きい数kと k+1番目の値で調整する
0.25 ✕ xk + 0.75 ✕ xk+1
となっています。
分かりにくいの具体的にやってみましょう!
データx(11個のデータ)で第1四分位点を定義通りに計算します。

まずは、「①k(データ数) – 1 」に 0.25, 0.5, 0.75を掛ける」です。
データ数は11なので
第1四分位数 10✕0.25 = 2.5
となります。
結果が2.5となったので
【整数+0.5】その数より1つ大きい数kと k+1番目の値で調整する
に該当します。
2.5より一つ大きい数は3なので、kは3、k+1は4となります。

それを以下の数式に当てはめると
0.5 ✕ xk + 0.5 ✕ xk+1
この数式に当てはめると
0.5 ✕ 169 +0.5 ✕ 171 = 170
となり、第1四分位点は170となります。
同じように、第3四分位数 10✕0.75 = 7.5
となるので

これも7.5なので
【整数+0.5】その数より1つ大きい数kと k+1番目の値で調整する
に当てはまって、
7.5より一つ大きい数は8、kは8、k+1は9となります。
つまり
0.5 ✕ 177 +0.5 ✕ 183 = 180
となり、第3四分位点は180となります。
念のため、データy(12個のデータ)でも同じ計算を行います。
まずはRで計算してみましょう!

最小値(0%)・第2四分位点/中央値(50%)・最大値(100%)は良いですね。
第1四分位点(25%)と第3四分位点(75%)を確認します。
定義通り、データの数12個から1引いた数11に0.25と0.75を掛けます。
第1四分位点 =>11✕0.25 = 2.75
第3四分位点 =>11✕0.75 = 8.25
第1四分位点の方は、2.75という数字が出ました。
これは、
【整数+0.75】その数より1つ大きい数kと k+1番目の値で調整する
0.25 ✕ xk + 0.75 ✕ xk+1
に当てはまりますね。

kは169、k+1も169となります。
計算式に当てはめて、
0.25 ✕ 169 +0.75 ✕ 169 = 169
第1四分位点は169となります。
同じように、第3四分位点は、8.25だったので、図のようにkは9、k+1は10となります。

計算は
【整数+0.25】その数より1つ大きい数kと k+1番目の値で調整する。
0.75 ✕ xk + 0.25 ✕ xk+1
に当てはまるので、
0.75 ✕ 177 +0.25 ✕ 183 = 178.5
となり、第3四分位点は178.5と計算されます。
Rで計算された結果と同じになりましたね(^o^)
その他の分位点
四分位数以外の中途半端なところでの分位数も計算してみましょう!
意味は無いですが63%でやってみます。
まずはRで計算

175.6になりました。
この計算方法は、四分位数の定義の応用でいけます。
まずは、63%点なので、データ数-1に対して0.63を掛けます。
63%点 => 10✕0.63=6.3
になるので、kは7、k+1は8となります。

あとは計算式をちょっと変えます。
こんな感じです。
0.7 ✕ xk + 0.3 ✕ xk+1
規則性分かりましたか?
(データ数-1)✕●%で計算した結果の少数部分に注目です。
ここでは0.3になったので、その例を使うと
kに掛けるのは、1から0.3引いた結果 0.7となります。
k+1にはそのまま0.3を掛けます。
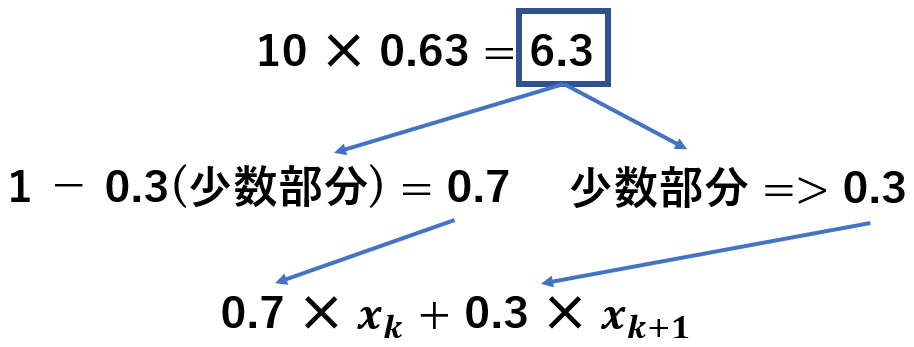
数値を当てはめて計算します。
0.7 ✕ 175 +0.3 ✕ 177 = 175.6
Rで計算したのと同じ結果が出ましたね(^o^)
おまけ
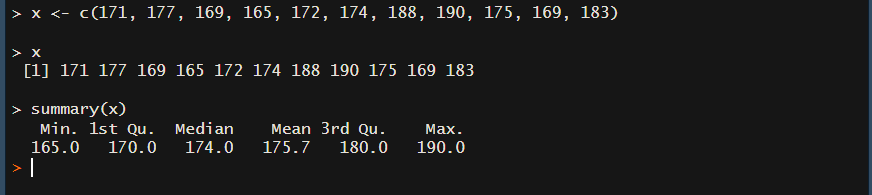
summary関数を使うことで、最小値・第1四分位数・中央値(第2四分位数)・平均・第3四分位数・最大値のデータを一気に出すことも出来ますので覚えておいて下さい(^o^)
summary(x)
まとめ
今回は、分位点について勉強しました!
実は四分位数の定義が色々あったので苦戦しましたw
コメント