はじめに
ひらちんです。
せっかく統計を勉強しているので、統計で出てくる計算をEXCELでやる時に使える関数や機能などをシリーズでお伝えします(^o^)
COVARIANCE.S関数
標本データから母集団の「共分散」を推定します。
共分散とは、2種類のデータの関係を示す指標です。
共分散が正の数になったときは、2つのデータに正の相関があり、負の相関があるときは共分散は負の数になります。
以前に、COVAR関数・COVARIANCE.P関数 で母集団の共分散を計算する方法を紹介しました。
ここでは、母集団が分からない場合などにサンプルから母集団の共分散を推定する方法を紹介します。
共分散は2つの変数の偏差の積の平均を計算することで求めることができます(^o^)
標本からの推定の場合は、データ数nで割るところを、n-1にします。
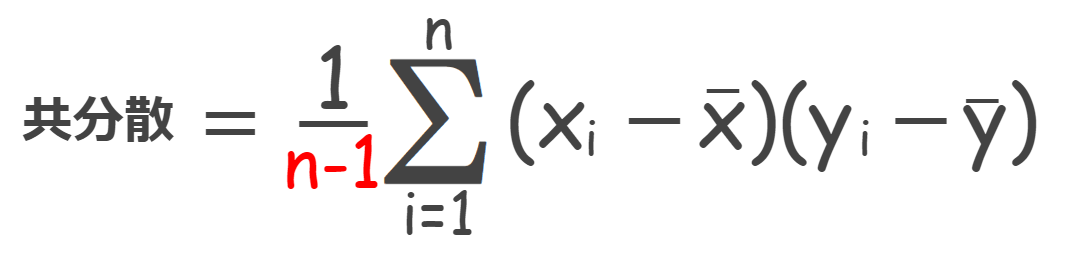
=COVARIANCE.S(配列1, 配列2)
引数の配列1と配列2に共分散を出したいデータを範囲で指定します。
「配列1」と「配列2」のデータ数は同じにする必要があるので注意してください。
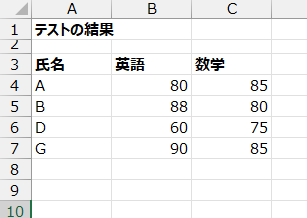
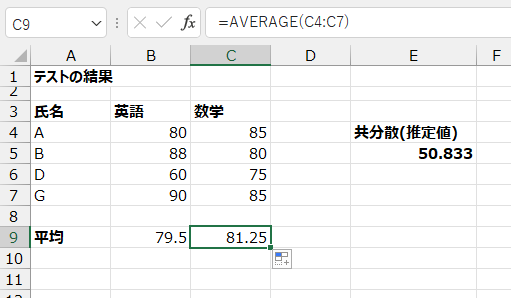
では、次の標本データで母集団の共分散を推定しましょう!
COVARIANCE.S関数の引数に必要なのは、
2つのデータの範囲(配列)です。
ここでは、英語の得点と数学の得点の範囲を指定します。
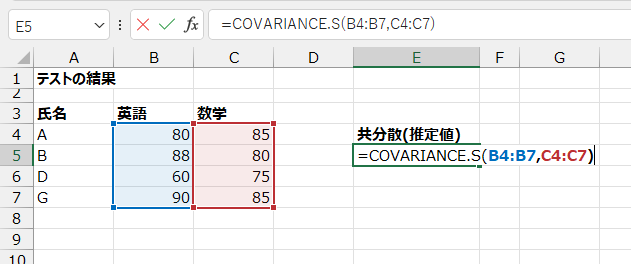
E5セルに、次の数式を入力します。
=COVARIANCE.S(B4:B7,C4:C7)
Enterで確定すると
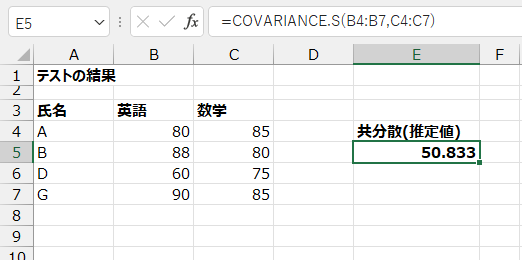
母集団の共分散の推定値は「50.833」と出ました。
COVARIANCE.S関数を使わずに計算した結果と比べてみましょう!
共分散は偏差の積の平均(推定の場合はデータ数をn-1で計算)なので、まずはそれぞれ偏差を計算しましょう!
英語・数学のそれぞれの平均値を9行目に計算します。
AVERAGE関数を利用します。

数学も同じようにします。
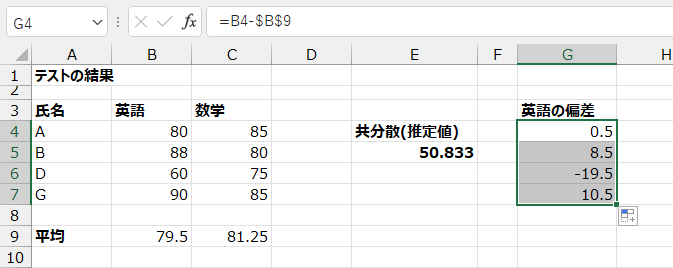
偏差は、各値とその平均値の差なので
G列に偏差を計算します。
G4セルに次の数式を入力し、下までコピーします。
=B4-$B$9
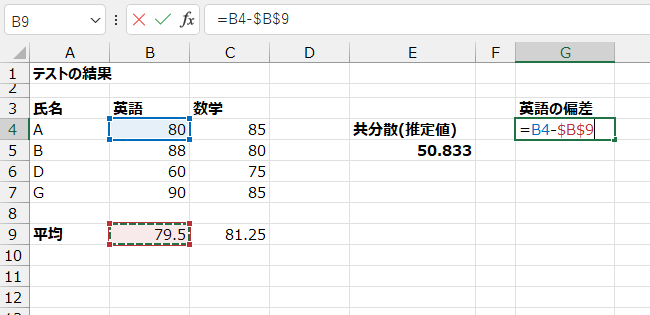
平均値は、下にコピーしたときにズレないように、絶対参照($)としています。
下までコピーします。
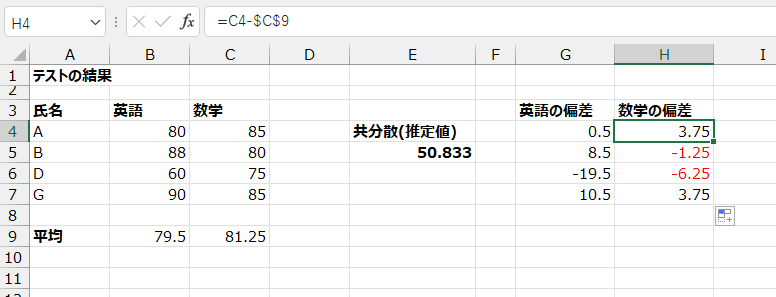
数学の偏差も同様に計算します。
英語の偏差と数学の偏差の積をI列に計算します。
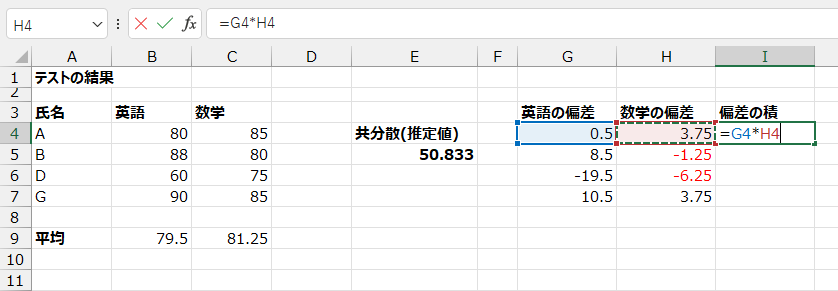
下までコピー
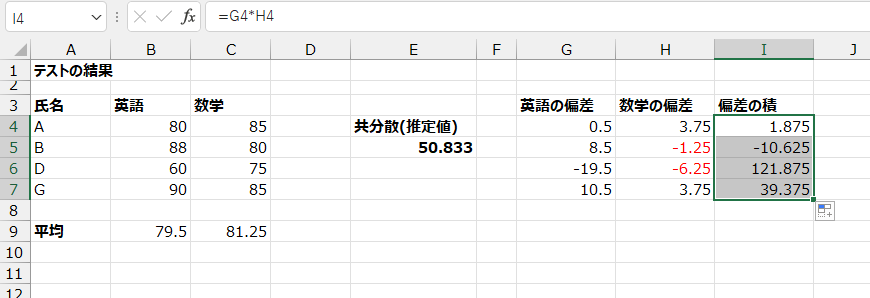
偏差の積の合計をI11セルに出します。
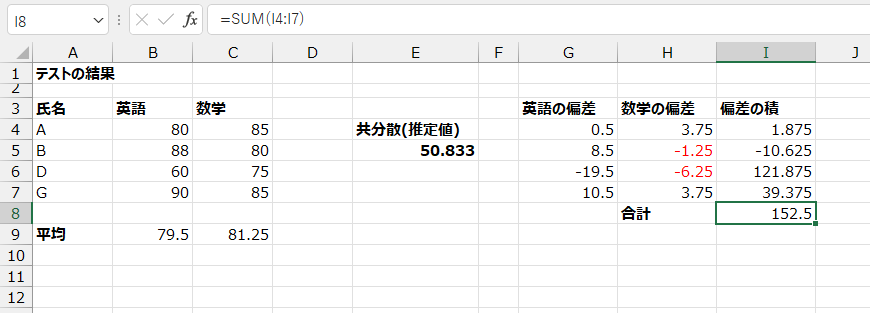
これを、データ数-1(ここでは3)で割ります。
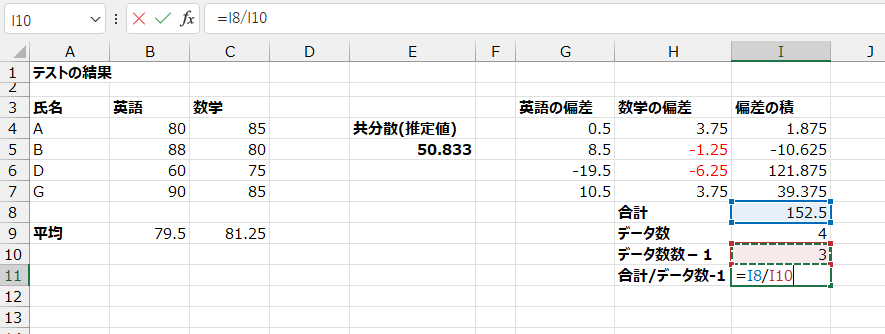
Enterで確定すると
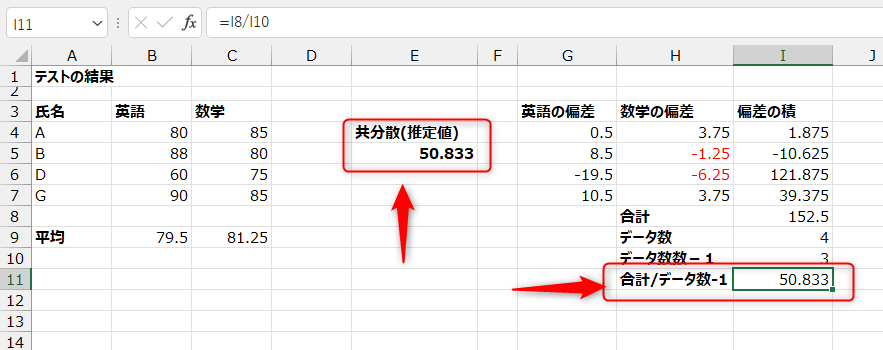
母集団の共分散の推定値が計算できました!
合ってますね(^o^)
以上です!
コメント