ポアソン分布
こんにちは!ひらちんです!Rを使った統計について自分の勉強も兼ねて記事にしています。
今回は、ポアソン分布についてです。
ポアソン分布ってなに?ということを順番に考えていきます。
ある学校の生徒数50人(n=50)のクラスで、1年間、欠席者の数を毎日記録していたデータがあるとします。
インフルエンザで大量に休みが出たというような特別な事情を別にすると日々の欠席率pは一定だと仮定できます。
ということは、確率pで起こる事象が、n=50の標本で起こる回数xの分布を考えることになりますね。
要は二項分布だよねって感じです。
ただし欠席率というケースの場合、お休みする生徒っていうのは毎日居るわけでもなく、居ても1人か2人って感じなので、確率としてはかなり小さい(稀な現象)と思われます。
仮に
確率 p=0.004
として、二項分布としてそのまま考えてみます。
n=50 なので、計算して表にすると
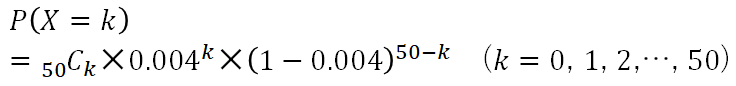
| 欠席者数 x | 確率 P(x) |
|---|---|
| 0 | 0.8184 |
| 1 | 0.1643 |
| 2 | 0.0162 |
| 3 | 0.0010 |
| 4 | 0.0000 |
| ~ | ~ |
| 46 | 0.0000 |
| 47 | 0.0000 |
| 48 | 0.0000 |
| 49 | 0.0000 |
| 50 | 0.0000 |
てことで、ほとんど0人で、1人はありそうだけど、2人になるのはすでに1.62%みたいな状態になってしまいます。
というか、組み合わせの計算とか地獄です。
そこで、もうちょっと簡単に計算出来へんのかな~っていうことで登場するのが ポアソン分布 です!
で、どういうものかと言うと
まず、二項分布に戻りますが、二項分布の期待値 E(X) は、
E(X) = np
で計算出来ます。
今回の例で言うと、
E(X) = 50✕0.004 = 0.2
ですね。
E(X) = np = μ (np=λ ってしてる場合も多い)
この期待値0.2を変えずに、nをどんどんどんどん大きくする(つまり、それに合わせてpを小さくしていく)と、以下の確率で表されるポアッソン分布になる。
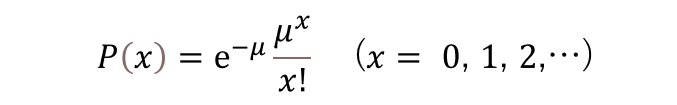
xは無限に大きくなっていくが、xが少し大きくなったらP(X)は、すぐにほとんど0になるので気にしない。
eは自然対数(ネイピア数)ので定数(2.71828‥)なので、この式P(X)は平均(期待値 E(X))だけで計算出来るってことになり、組み合わせの数の計算から開放されます!
加えて、計算するときに確率pも、標本数nも使わないっていうことは、nがめっちゃ大きくて、pがめっちゃ小さいときは、確率や標本数がちょっとくらい変動しても関係ねー!ってことになりますね。
では、さっきの欠席者数の確率計算をこれでしてみましょう!
| 欠席者数 x | 計算式 | 確率 P(x) ※ポアソン | 確率 P(x) ※元 |
|---|---|---|---|
| 0 | e^(-0.2) ✕ 0.2^0 | 0.8187 | 0.8184 |
| 1 | e^(-0.2) ✕ 0.2^1 ÷ 1 | 0.1637 | 0.1643 |
| 2 | e^(-0.2) ✕ 0.2^2 ÷ 2! | 0.0164 | 0.0162 |
| 3 | e^(-0.2) ✕ 0.2^3 ÷ 3! | 0.0011 | 0.0010 |
| 4 | e^(-0.2) ✕ 0.2^4 ÷ 4! | 0.0000 | 0.0000 |
| ~ | ~ | ~ | ~ |
| 49 | e^(-0.2) ✕ 0.2^49 ÷ 49! | 0.0000 | 0.0000 |
| 50 | e^(-0.2) ✕ 0.2^50 ÷ 50! | 0.0000 | 0.0000 |
大体一緒!ということです(^o^)
Rで計算してみる
では、ポアソン分布の確率密度をRを使って計算してみます!
Rでポアソン分布のあれこれをいじる場合は、 *pois関数 を使います。
| 分布名 | ランダム値 | 密度 | 分布 | 分位点 |
|---|---|---|---|---|
| ポアソン分布 | rpois関数 | dpois関数 | ppois関数 | qpois関数 |
ランダム値 rpois関数
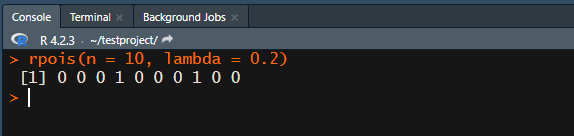
ポアソン分布に従う数値をランダムに抽出する場合は、 rpois関数 を使います。
rpois(n = 10, lambda = 0.2)
nは、抽出したい数 lambdaは “λ” つまり平均(期待値)を指定します。
いくつか lambda の値を変えて抽出したものをグラフにしてみます。
λを1,3,5,15,30と変えてそれぞれ10000個抽出して、それぞれグラフにして見比べます。
# λの指定を変えたデータを取得
pois1 = rpois(n = 10000, lambda = 1)
pois3 = rpois(n = 10000, lambda = 3)
pois5 = rpois(n = 10000, lambda = 5)
pois15 = rpois(n = 10000, lambda = 15)
pois30 = rpois(n = 10000, lambda = 30)
# データフレームに結合
pois <- data.frame(Lambda.1=pois1, Lambda.3=pois3,
Lambda.5=pois5, Lambda.15=pois15, Lambda.30=pois30)
# フォーマットの変換
require(reshape2)
pois <- melt(data = pois, variable.name = "Lambda", value.name = "x")
# 扱える数値に変換
require(stringr)
pois$Lambda <- as.factor(as.numeric(str_extract(string = pois$Lambda,
pattern = "\\d+")))
# グラフの作成
require(ggplot2)
ggplot(pois, aes(x = x)) + geom_histogram(binwidth = 1) +
facet_wrap(~Lambda) + ggtitle("λごとのヒストグラム")出来たグラフはこちらです。
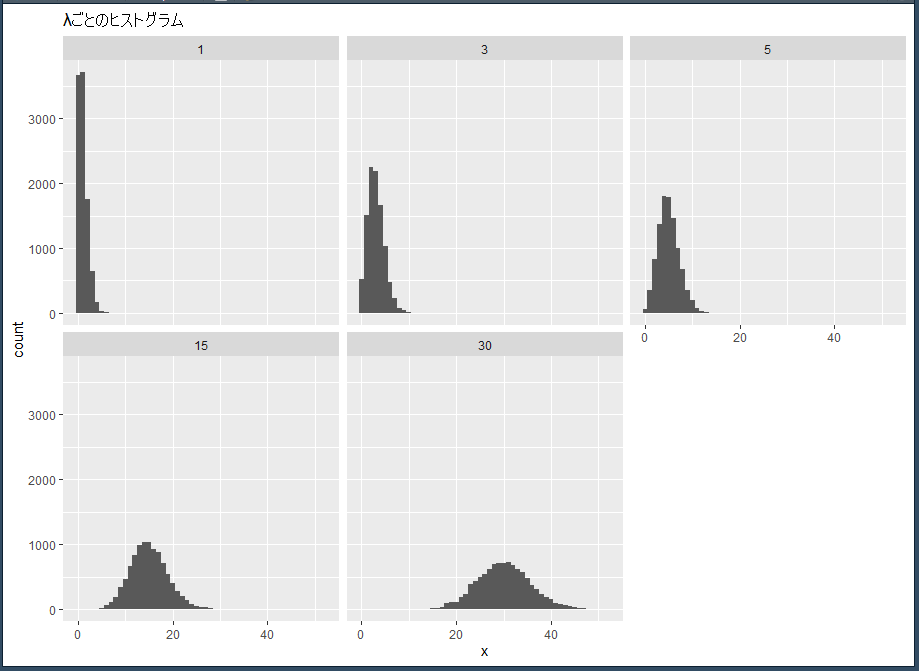
λが大きくなると、正規分布に近づいていきます。
グラフ作成部分を修正して、重ねて表示します。
# グラフの作成(重ねて表示)
require(ggplot2)
ggplot(pois, aes(x = x)) +
geom_density(aes(group =Lambda, colors = Lambda, fill = Lambda) ,
adjust = 4, alpha = 1/2) +
scale_color_discrete() + scale_fill_discrete() +
ggtitle("λごとのヒストグラム")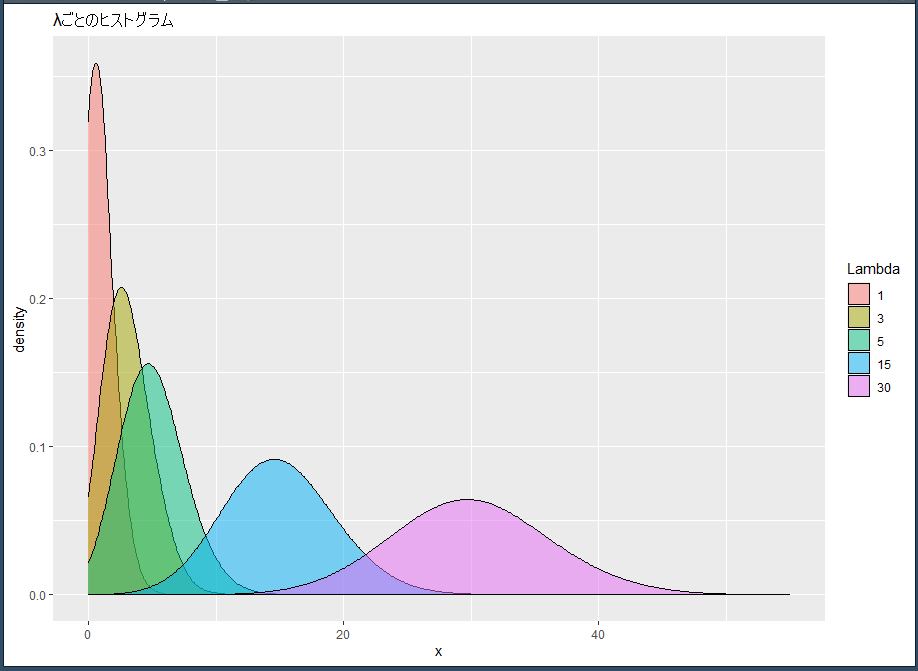
より分かりやすいですね(^o^)
確率密度の計算 dpois関数
表2で電卓で計算した数式
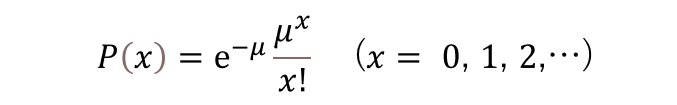
こいつを計算するには、 dpois関数 を使います。
dpois(x = 0, lambda = 0.2)
xに確率密度を求めたいxを指定し、lambdaにはλ(上の数式ではnp=μ)を指定します。
| 欠席者数 x | 確率 P(x) |
|---|---|
| 0 | 0.8187 |
| 1 | 0.1637 |
| 2 | 0.0164 |
| 3 | 0.0011 |
| 4 | 0.0000 |
| ~ | ~ |
| 49 | 0.0000 |
| 50 | 0.0000 |
表3と同じようになるか、Rで計算してみましょう。
まずは x=0

良いですね。
次は x=1

良いですね
x=2~10まで一気に
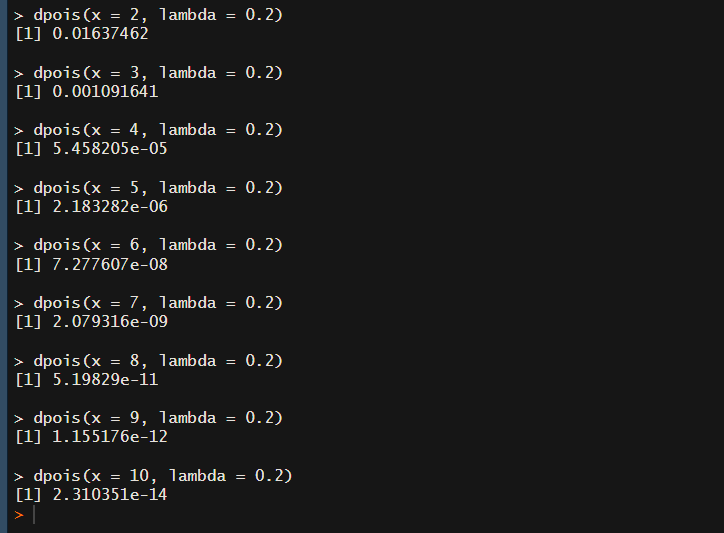
完璧です。
累積確率の計算 ppois関数
ポアソン分布の累積確率を計算するには、 ppois関数 を使います。
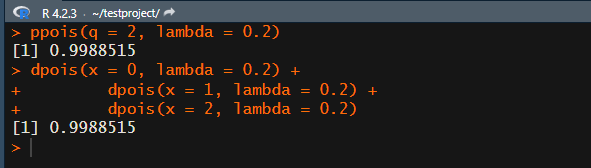
では、例として λ=0.2, x=2以下の累積確率を計算します。
ppois(q = 2, lambda = 0.2)
q にどこまでのxかを指定、lambdaはλを指定します。

一個ずつ足したのと一致します。
まとめ
今回は、Rでポアソン分布について勉強しました。
よーし、どんどん頑張るぞ!
コメント