はじめに
こんにちは!ひらちんです!Rを使った統計について自分の勉強も兼ねて記事にしています。
今回は、相関と共分散についてです!
相関とは
相関とは、対になっている2つのデータが一方が変化した時に他方も変化するように、相互に関係しあっていることを言います。
統計では、これを相関係数という指標で表します。
相関係数を計算する公式は以下のようになります。
【対象データが母集団全体の場合】
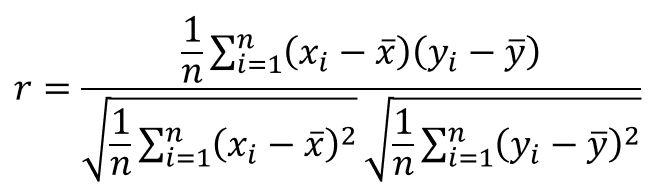
【対象データが母集団からのサンプルの場合】
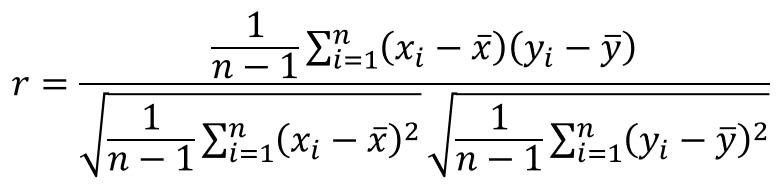
公式の分母の部分を見て下さい。
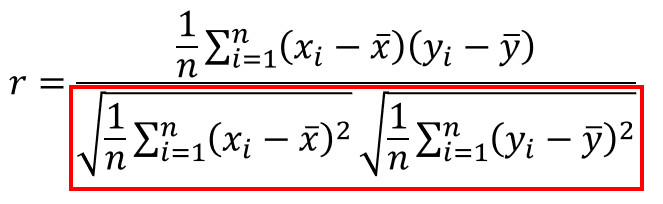
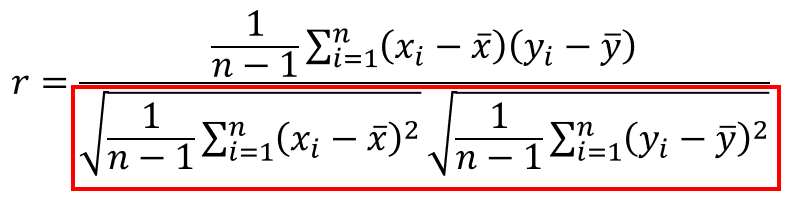
これはそれぞれ、データxとyの標準偏差になっていますね。
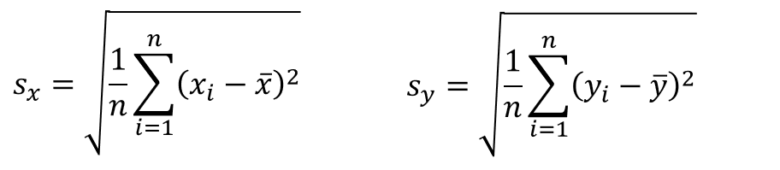
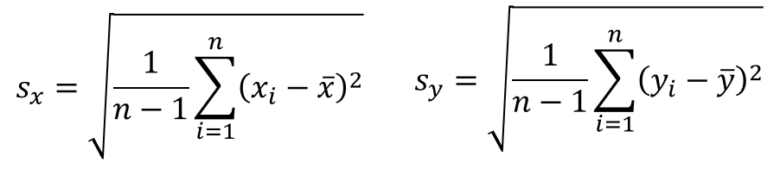
次に分子の部分です。
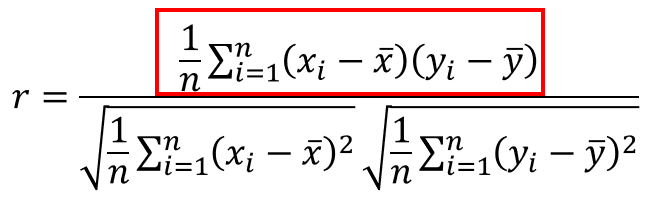
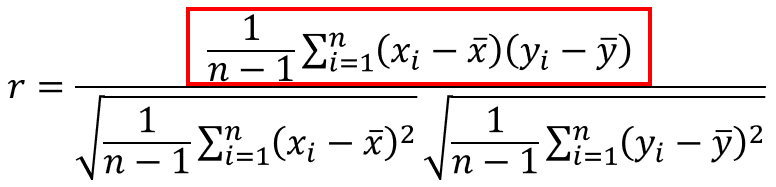
これは、後で出てくる共分散になります。
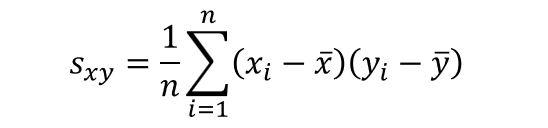
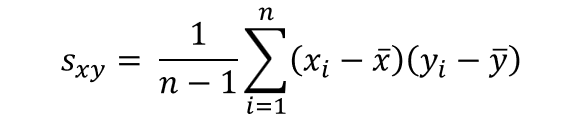
つまり、相関係数は
になっています。
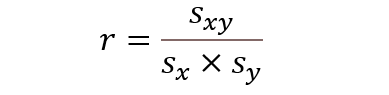
共分散とは
では、次に共分散についてです。
共分散とは、2組の対応するデータの関係表す指標です。
共分散を求めるには、2つの変数の偏差の積の平均を計算します。
相関係数との違いは、相関係数の値が-1から0の間を取るのに比べて、共分散はそうとは限らないというところです。
相関係数のところで出てきた数式の再掲です。
【データが母集団全体を対象にしている場合】
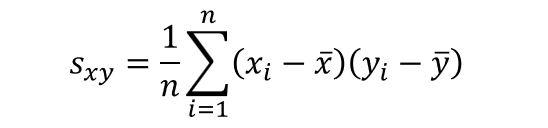
【データが母集団からのサンプルを対象にしている場合】
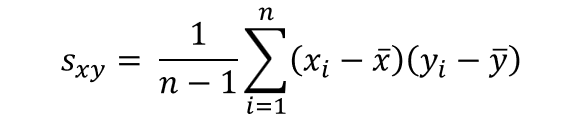
また、次の公式でも求めることが出来ます。
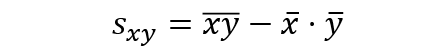
xとyの積の平均から、それぞれの平均の積を引いたものです。
こっちの方が計算が楽かもしれないですね。
Rで相関係数を計算する
Rで相関係数を計算するには、 cor関数 を使います。
ggplot2パッケージの中のeconomicsデータを使います。
require(ggplot2)
head(economics)実行すると次のような結果が出力されます。
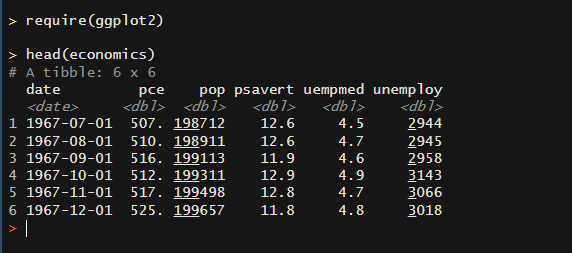
カラムのpceは個人消費支出、psavertは個人貯蓄率です。
この2つの相関関係を計算してみます。
先程のコードの続きに
cor(economics$pce, economics$psavert)
を追加して下記のようにして実行します。
require(ggplot2)
head(economics)
cor(economics$pce, economics$psavert)結果は以下のようになります。

-0.7928546とかなり低い相関係数になりました。
消費と貯蓄は相反する関係になっているので納得出来ますね(^^)
Rで共分散を計算する
Rで共分散を計算するには、 cov関数 を使います。
先程と同じく、ggplot2パッケージの中のeconomicsデータを使います。
require(ggplot2)
head(economics)このコードの続きに
cov(economics$pce, economics$psavert)
を追記して実行します。
require(ggplot2)
head(economics)
cov(economics$pce, economics$psavert)結果は以下のようになります。
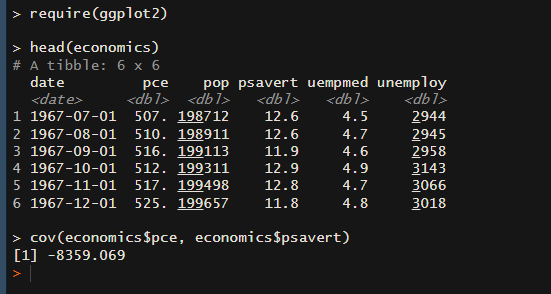
-8359.069ですね。
マイナスの数値が出ているので、これはpceが増加すると、psavertが現象するような関係にあるといえます。
検算
念のため、他の計算方法でも同じ結果になるか分解して計算してみましょう!
以下は最初に紹介した、相関係数を計算する公式(対象データが母集団からのサンプルの場合)の再掲です。
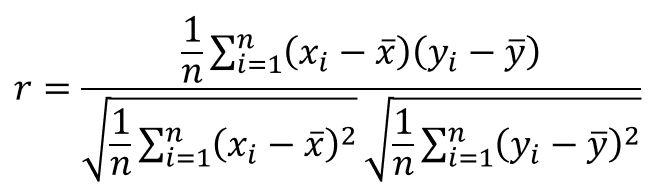
これに沿って分解していきましょう!
この公式は、以下のように組みたっていました。

まずは、分子にある x(pce)とy(psavert)の共分散を cov関数 を使わずに計算します。
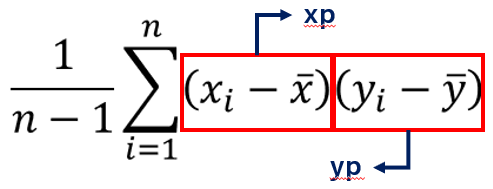
![]() をxp、
をxp、![]() をypとして新たな列を作成します。
をypとして新たな列を作成します。
xp <- economics$pce – mean(economics$pce)
yp <- economics$psavert – mean(economics$psavert)
をコードに追加します。
require(ggplot2)
head(economics)
xp <- economics$pce - mean(economics$pce)
yp <- economics$psavert - mean(economics$psavert)次に、n-1 つまりデータ数引く1を計算しておきます。
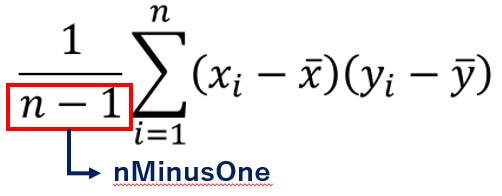
データの行数を計算するには、 nrow関数 を使います。
先程のデータの続きに
nMinusOne <- (nrow(economics) – 1)
を追記します。
require(ggplot2)
head(economics)
xp <- economics$pce - mean(economics$pce)
yp <- economics$psavert - mean(economics$psavert)
nMinusOne <- (nrow(economics) - 1)これで共分散を計算する材料はそろいました。
では計算します。
sum(xp * yp) / nMinusOne
xp と yp をかけたものを合計して、nMuinusOneで割ればいいですね(^^)
コードに追記して実行します。
require(ggplot2)
head(economics)
xp <- economics$pce - mean(economics$pce)
yp <- economics$psavert - mean(economics$psavert)
nMinusOne <- (nrow(economics) - 1)
sum(xp * yp) / nMinusOne結果は以下のようになります。
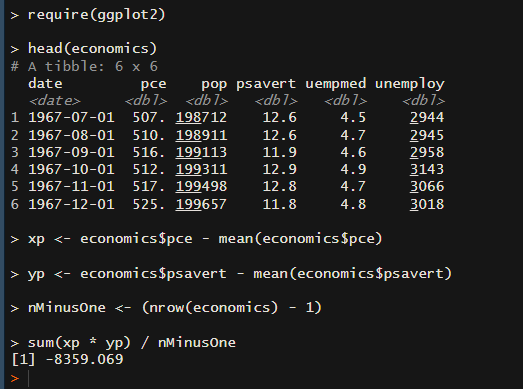
-8359.069 で、 cov関数 で計算したときと同じになりましたね!
続いて、分母の x(pce)とy(psavert) それぞれの標準偏差を計算します。

xの標準偏差
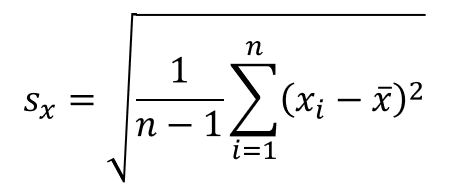
これの![]() の部分は、先程 xp として計算しました。
の部分は、先程 xp として計算しました。
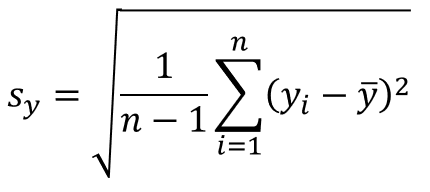
これの![]() の部分も同じですね。
の部分も同じですね。
材料は揃っているので、計算しちゃいましょう!
xの標準偏差を、sd_pce yの標準偏差を sd_psavert とします。
あ、ついでにさっき計算したxとyの共分散も cov_pce_psavert として変数に入れておきます。
次のコードを追記します。
cov_pce_psavert <- sum(xp * yp) / nMinusOne
sd_pce <- sqrt(sum(xp ^ 2) / nMinusOne)
sd_psavert <- sqrt(sum(yp ^ 2) / nMinusOne)
Rで2乗を計算するには、「x ^ 2」か「x ** 2」とチルダかアスタリスク2個を使います。
また、平方根の計算には、 sqrt関数 を使います。
今、コードはこんな感じ
require(ggplot2)
head(economics)
xp <- economics$pce - mean(economics$pce)
yp <- economics$psavert - mean(economics$psavert)
nMinusOne <- (nrow(economics) - 1)
cov_pce_psavert <- sum(xp * yp) / nMinusOne
sd_pce <- sqrt(sum(xp ^ 2) / nMinusOne)
sd_psavert <- sqrt(sum(yp ^ 2) / nMinusOne)最後に、cov_pce_psavert と sd_pce と sd_psavert を使って、相関係数を計算します。
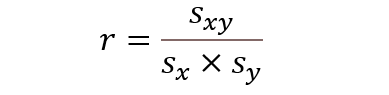
これなので、
cov_pce_psavert / (sd_pce * sd_psavert)
これですね。
コードに追記して最終はこんな形になります。
実行しましょう!
require(ggplot2)
head(economics)
xp <- economics$pce - mean(economics$pce)
yp <- economics$psavert - mean(economics$psavert)
nMinusOne <- (nrow(economics) - 1)
cov_pce_psavert <- sum(xp * yp) / nMinusOne
sd_pce <- sqrt(sum(xp ^ 2) / nMinusOne)
sd_psavert <- sqrt(sum(yp ^ 2) / nMinusOne)
cov_pce_psavert / (sd_pce * sd_psavert)実行結果は
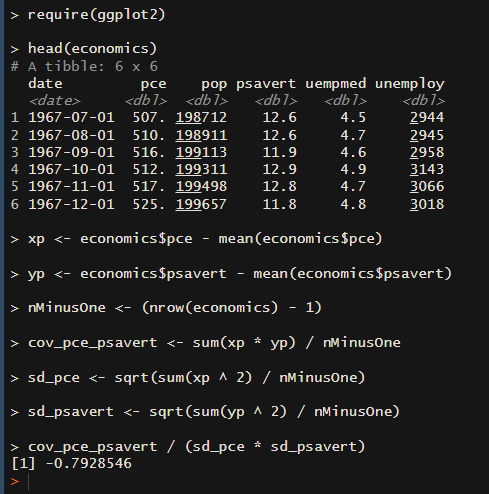
-0.7928546 と cor関数 で計算した結果と同じになりました!
まとめ
今回は、相関と共分散について勉強しました!
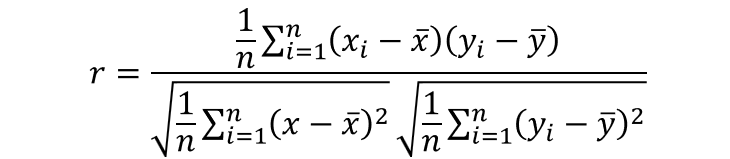
コメント