はじめに
こんにちは!ひらちんです!Rを使った統計について自分の勉強も兼ねて記事にしています。
今回は、平均(算術平均)の計算についてです!
平均(算術平均)
データの平均(算術平均)を計算するには、 mean関数 を利用します。
まずは、単純な算術平均を計算します。
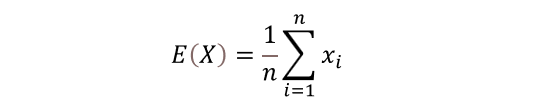
計算に必要なサンプルを作るには、 sample関数 が便利です。
sample(x=1:20, size=20, replace=TRUE)
これで、1から20の間でランダムに20個選んでくれます。
replaceの引数は、選ぶ数字の重複がOKかどうかです。
ここでは、TRUEにしているので重複OKとなります。

データにNA(欠損値)がない場合の平均
では、作成したサンプルから平均を計算しましょう。
mean(x)
これだけです。

簡単ですね。
データにNA(欠損値)が入っている場合
データの中にNA(欠損値)が入っている場合がありますよね。
先程抽出したサンプル「x」のうちランダムに5個をNA(欠損値)に置換します。
y <- x y[sample(x = 1:20, size=5, replace=FALSE)] <- NA

この場合、そのまま mean関数 に入れると NA が返ってきてしまいます。

NA(欠損値)を含む場合は、引数 na.rm = TRUE を指定します。
mean(y, na.rm = TRUE)

このサンプルで言うと
156÷15=10.4
が返ってきます。
加重平均(重み付け平均)
加重平均とは、数値の重みを考慮して平均値を求める算出方法で、「重みつき平均」と言われることもあります。
売上金額やアンケート結果の平均などで利用されます。
例えば、ひらちんショップでの1日の売上で以下のような結果があったとします。
| 商品名 | 単価 | 販売数 |
|---|---|---|
| ひらちんの剣 | 30,000 | 15 |
| ひらちんの盾 | 25,000 | 20 |
| ひらちんの鎧 | 35,000 | 18 |
ここから、1日の1商品あたりの平均売上を求める場合、
剣:30,000 + 盾:25,000 + 鎧:35,000 = 合計:90,000 90,000 ÷ 3 = 30,000
とするのは間違いですね。
販売数の違い(数値の重み)が考慮されていません。
この場合、加重平均を利用して
販売数合計=剣:15 + 盾:20 + 鎧:18 = 53 売上合計 =剣:30,000✕15 + 盾:25,000✕20 + 鎧:35,000✕18 = 1,580,000 売上合計 ÷ 販売数合計 = 29811.320‥
とします。
Rでこの加重平均を計算するには、 weighted.mean関数 を使います。
weighted.mean(x=grades,w=weights)
引数のxとwには、平均を計算するベクトルと重み付けのベクトルを用意します。
では、先程のひらちんショップの売上で計算してみましょう。
# 商品の売上単価のベクトル
grades <- c(30000,25000,35000)
# 重み付けのベクトル
weights <- c(15/60, 20/60, 18/60)
# 加重平均の計算
weighted.mean(x=grades,w=weights)こんな感じになります。
それでは実行してみましょう!
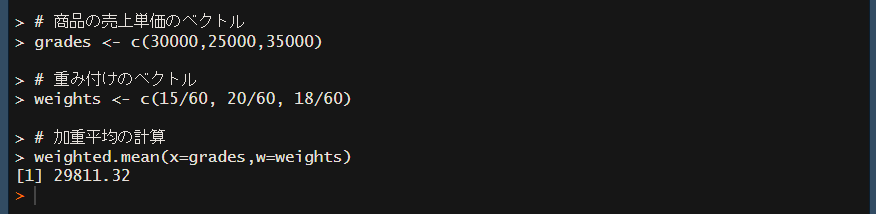
先程計算した結果と同じになりましたね(^o^)
まとめ
今回は、Rで平均について勉強しました。
引き続き頑張ります!
コメント